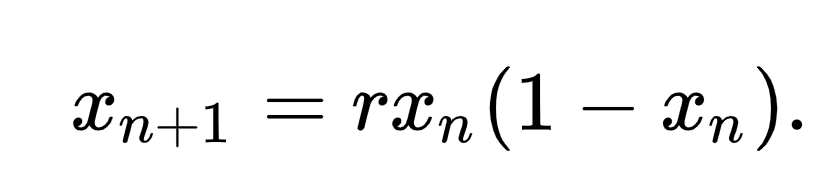Sometimes simple things show complex behavior when you expect them not to - I find that really interesting.
Sure, it’s simple to think that that chaotic systems with many degrees of freedom would yield complex behavior; and in most cases that’s true. However, the same can be true of incredibly simple models, in ways which feel unintuitive. In a single, one-line equation, not only is chaos found, but also order. The variables seem to ebb and flow between complete randomness and absolute stability in a way that has structure and some kind of logic. How can this be?
Bifurcations originating from simple bounded population growth.
Logistic map
Interesting behavior can come from uninteresting equations. The logistic map is shown above and it can be applied to any number of applications or situations. Many people tend to think of this in an example centered on bounded population growth. Let’s think of a population of animals which can vary over time, and their population fraction as being from 0 to 1, where 1 represents the maximum number of animals which can be supported by their environment. This equation says that the birth rate (r) relates the population fraction next year (xn+1) to the population fraction this year (xn). In other words, if our animals are really good at making babies, and the environment can support it, the population will grow until it reaches a steady state where births and deaths are balanced. This is all well and good, but the question becomes, how does the ability of the animals to mate (i.e. the growth rate) impact the equilibrium population fraction in the end? Of course, if the rate is less than 1, the population has more deaths than births, thus dying out in a few generations - meaning that the stable population fraction is always zero. Above 1, the population will grow because the births outweigh the deaths, just as we suspect. However, when growth rates exceed 3, something wild happens. The population stability spontaneously splits into an oscillation between two states, one increasing with growth rate and one decreasing with growth rate. This continues until ~3.45, at which point the oscillation splits again, into four states, before splitting into 8, and so on. Until chaos happens. Complete randomness without predictability, which unintuitively and fleetingly descends into order once again. These cycles persist, on and on, between order and disorder, seemingly violating the laws of entropy until the growth rate reaches ~4. Amazingly, at a growth rate of 3.9998 the population converges to a stable fraction of 0.17, whereas at 3.9999 the population reaches close to 1, incredible instability and randomness. But just before that, close to growth rates of 3.83, the population falls into total 3-frequency oscillatory predictability with final stable points near 0.95, 0.5, and 0.15 for population fraction. Somehow, at this point, the population can only occupy one of those three states. Whereas later on, the randomness seems to reemerge. I’m not a mathematician but this is amazing to me and I love thinking about it.
wtf this is awesome